State and Explain Hooke’s Law| Application | Disadvantages

State and Explain Hooke’s Law

“Hooke’s Law states that the force needed to extend or compress a spring by some distance is proportional to that distance.”

Mathematically, it can be expressed as:

[ F = -kx ]

Where:

• ( F ) is the force applied to the spring,
• ( k ) is the spring constant, which represents the stiffness of the spring,
• ( x ) is the displacement from the spring’s equilibrium position.

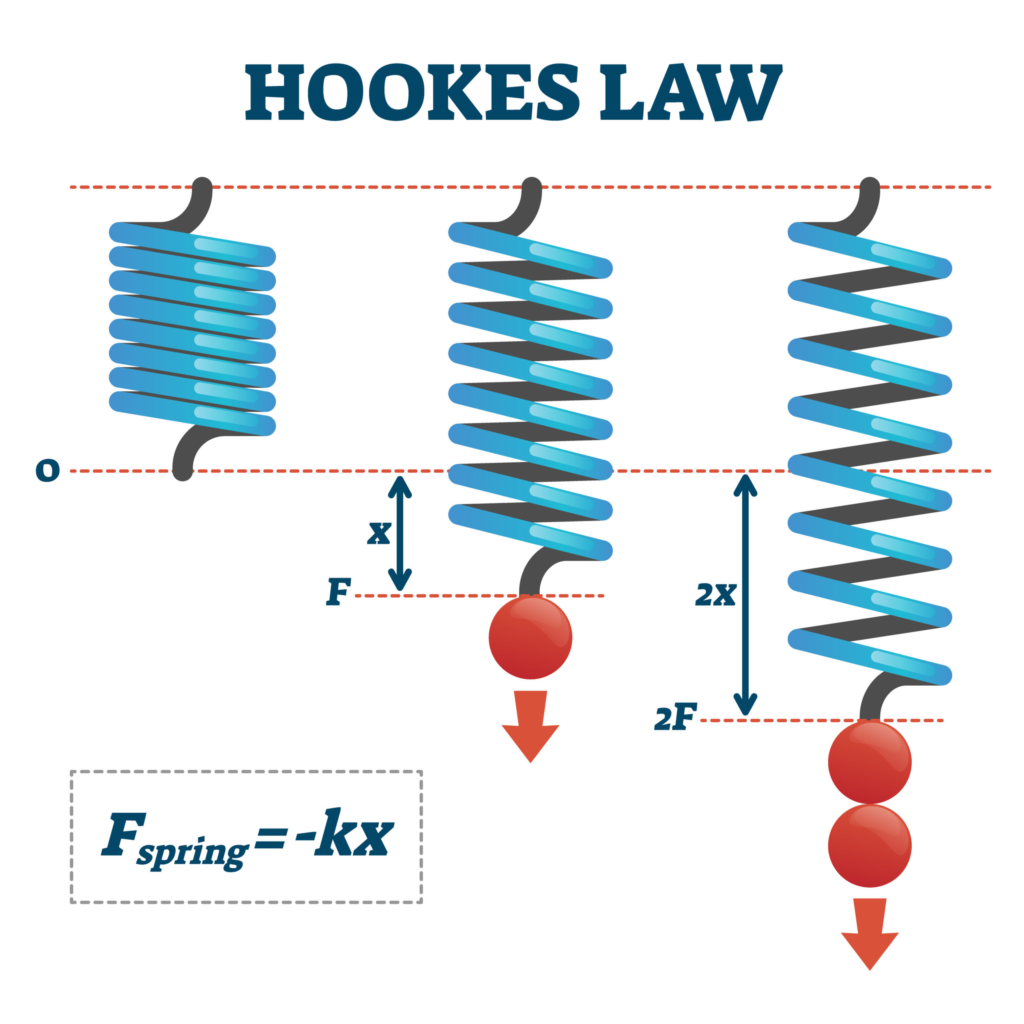
This law applies within the elastic limit of a material, meaning it’s valid only as long as the material returns to its original shape and size after the stress is removed.

Hooke’s Law can be explained through the behavior of the atomic or molecular bonds within the material. When a force is applied to stretch or compress a material, the bonds between the atoms or molecules within the material are either stretched or compressed. These bonds act like tiny springs.

Initially, when a small force is applied, the material responds linearly, meaning the extension or compression is directly proportional to the force applied, in accordance with Hooke’s Law. However, once the force exceeds a certain limit, known as the yield point, the material becomes permanently deformed, and Hooke’s Law no longer applies.

Hooke’s Law is fundamental in many areas of science and engineering, including mechanics, materials science, and civil engineering, and it’s used to analyze and design various structures and systems.

Also Read: Coulomb’s Law

History of Hooke’s law

Hooke’s Law is named after Robert Hooke, an English scientist who formulated it in the 17th century. Hooke was a polymath known for his contributions to physics, astronomy, biology, and engineering.

The law was first described by Hooke in 1660 in his work “De Potentia Restitutiva,” which was later expanded upon in his famous publication “Micrographia” in 1665. In “Micrographia,” Hooke presented various scientific observations and experiments, including his study of springs and the elasticity of materials.

Hooke’s inspiration for the law came from his observations of the behavior of springs and elastic materials. He noticed that when a spring was stretched or compressed, it exerted a restoring force that was proportional to the displacement from its equilibrium position. This led him to formulate the fundamental relationship between the force applied to a spring and the resulting displacement, which became known as Hooke’s Law.

Hooke’s Law was a significant breakthrough in understanding the mechanical properties of materials. It provided a mathematical framework for describing the behavior of elastic materials under stress and laid the foundation for the development of elasticity theory. Hooke’s work had profound implications for various fields of science and engineering, influencing advancements in mechanics, materials science, and structural engineering.

Hooke’s law applications

• Spring systems: Designing and analyzing mechanical devices like shock absorbers and suspension systems.
• Materials testing: Characterizing material properties such as stiffness through controlled stress and strain measurements.
• Structural analysis: Predicting deformations and stresses in beams, columns, and frames to ensure structural integrity.
• Force measurement: Utilizing load cells and strain gauges to measure force based on the deformation of elastic elements.
• Vibration analysis: Understanding the response of mechanical systems to vibrations and designing damping mechanisms.
• Biomechanics: Studying the mechanical properties of biological tissues and structures, aiding in orthopedic design and sports biomechanics.

Hooke’s law disadvantages

• Validity within elastic limit: Limited to materials exhibiting linear elastic behavior, becoming inaccurate beyond the elastic limit.
• Material dependency: Assumes uniform and isotropic behavior, not suitable for complex materials like composites.
• Temperature and environmental effects: Does not account for variations due to temperature, humidity, or chemical exposure.
• Nonlinear behavior: Inadequate for materials with nonlinear stress-strain relationships under high loads or complex conditions.
• Creep and fatigue: Fails to address time-dependent phenomena such as creep and fatigue, crucial for long-term material performance.
• Complex structures: Provides a simplified approach, may not suffice for analyzing complex structures requiring advanced methods.